Bạn đang quan tâm đến Định nghĩa, tính chất & cách chứng minh các Tam giác đặc biệt phải không? Nào hãy cùng VCCIDATA đón xem bài viết này ngay sau đây nhé, vì nó vô cùng thú vị và hay đấy!
XEM VIDEO Định nghĩa, tính chất & cách chứng minh các Tam giác đặc biệt tại đây.
Hình học là một môn học quan trọng trong trường học và có nhiều ứng dụng liên quan đến cuộc sống hàng ngày. tuy nhiên, nhiều em vẫn chưa biết phương pháp tư duy và học tập hiệu quả, điều này tạo nên lỗ hổng kiến thức về hình học. vì vậy gia sư việt xin giới thiệu bài: định nghĩa, tính chất, cách chứng minh tam giác đặc trong môn hình học 7. đây là dạng kiến thức cơ bản các em học sinh sẽ theo sát đến lớp 12 nên các em cần theo dõi từ gần đến trang bị cho mình những hiểu biết đúng đắn về nó.
i. tam giác cân
1. định nghĩa của tam giác cân
tam giác cân là tam giác có hai cạnh bằng nhau.
Bạn đang xem: Tam giác vuông là tam giác gì
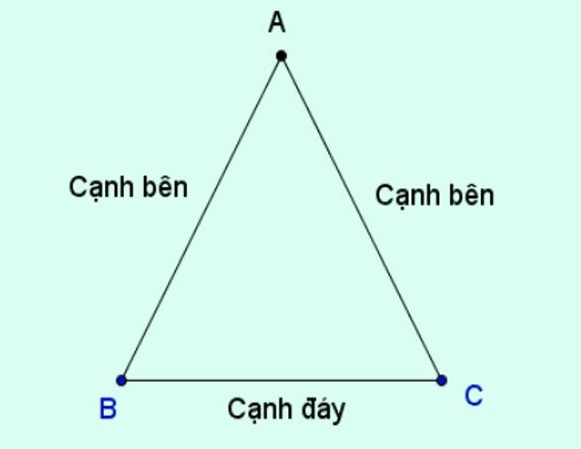
Từ hình này, chúng tôi có thể xác định:
– đỉnh a của tam giác cân abc là giao điểm của hai cạnh ab và ac.
– Góc a được gọi là góc trên, hai góc b và c còn lại là góc ở đáy.
cách tạo tam giác cân abc trong a
– vẽ đường viền bc
– vẽ một cung tròn với tâm b, bán kính r
– vẽ một cung tròn với tâm c, bán kính r
hai cung cắt nhau tại a.
tam giác abc là tam giác cần vẽ.
2. thuộc tính của tam giác cân
– tính chất 1: trong một tam giác cân, hai góc ở đáy bằng nhau.
ví dụ: hình tam giác oab là cân tại o = & gt; góc a = b
– tính chất 2: tam giác có hai góc bằng nhau là tam giác cân.
ví dụ: hình tam giác có góc o = d = & gt; phần thân của tam giác cân ở b
– thuộc tính 3: trường hợp đặc biệt của tam giác cân:
Tam giác vuông cân là tam giác vuông có hai góc vuông bằng nhau.
ví dụ: tam giác vuông mnp tại m có góc n = p = & gt; tam giác mnp tạo thành một góc vuông tại m
tính số đo của mỗi góc nhọn của tam giác vuông cân.
ta có: abc có góc a = 90 °, góc b = c
= & gt; góc b + c = 90 ° (định lý tổng tam giác)
= & gt; 2. Ĉ = 90 °
= & gt; góc b = c = 45 °
kết luận: nếu một tam giác vuông cân thì hai góc nhọn bằng 45 °.
3. cách chứng minh tam giác cân
– cách 1: Chứng minh tam giác có hai cạnh bằng nhau.
– Cách 2: Chứng minh tam giác có hai góc bằng nhau.
chẳng hạn, trong tam giác abc có Δ Abd = Δ acd. Chứng minh rằng tam giác abc là cân.
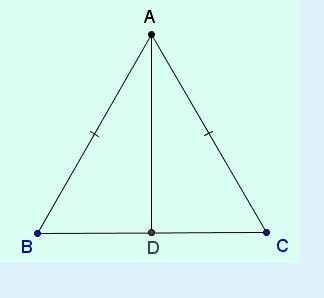
+ thử biểu mẫu 1:
theo bài báo, chúng tôi có:
Xem ngay: Cách đánh điệu slow guitar
Abd = acd
= & gt; ab = ac
= & gt; tam giác abc cân tại a
+ thử cách 2:
theo bài báo, chúng tôi có:
∆abd = acd
= & gt; góc b = c
= & gt; tam giác abc cân tại a
ii. tam giác đều
1. định nghĩa của một tam giác đều
Tam giác đều là tam giác có ba cạnh bằng nhau.
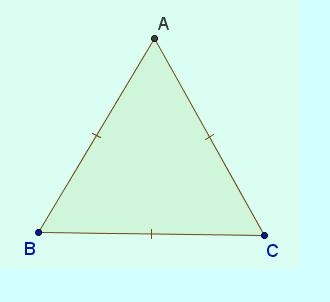
cách xây dựng một tam giác đều abc
– vẽ đường viền bc
– draw (b; bc) and (c; bc)
– (b; bc) (c; bc) trong a
abc là một tam giác đều để vẽ.
2. tính chất của tam giác đều
– tính chất 1: trong một tam giác đều, mỗi góc đo được 60 độ
ví dụ: tam giác đều oab = & gt; góc a = o = b = 60 °
– tính chất 2: một tam giác đều có 3 đường cao bằng nhau
– tính chất 3: một tam giác đều có 3 trung tuyến bằng nhau
3. cách chứng minh tam giác đều
– Phương pháp 1: Chứng minh tam giác có 3 cạnh bằng nhau.
ví dụ: hình tam giác oab với oa = ob = ab
= & gt; tam giác đều oab
– Phương pháp 2: Chứng minh tam giác có 3 góc bằng nhau.
ví dụ: thử hình tam giác oab với góc o = b = a
= & gt; tam giác đều oab
– Phương pháp 3: Chứng minh tam giác cân và có một góc bằng 60 độ.
ví dụ: hình tam giác oab với oa = ob và o = 60 °
= & gt; tam giác đều oab
– Phương pháp 4: Chứng minh tam giác có 2 góc bằng 60 độ.
ví dụ: hình tam giác oab có góc a = b = 60 °
= & gt; tam giác đều oab
iii. tam giác vuông
1. định nghĩa tam giác vuông
Xem thêm: Nguyên tắc hoạt động liên tục là gì
Tam giác vuông là tam giác có một góc vuông (góc 90 °).
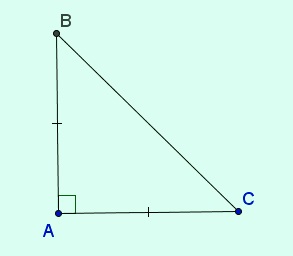
cách tạo tam giác vuông abc trong a
cho cạnh huyền bc = 4,5 cm và cạnh bên góc vuông ac = 2 cm.
– xây dựng ac = 2 cm
– đặt góc cax thành 90o.
– Dựng một đường tròn có tâm c và bán kính 4,5 cm, cắt trục ở b. tham gia vì chúng tôi có abc để xây dựng.
2. tính chất của tam giác vuông
– tính chất 1: trong một tam giác vuông, hai góc nhọn bù nhau.
ví dụ: tam giác vuông oab in o
= & gt; góc a + b = 90 °
– tính chất 2: trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương của hai cạnh.
ví dụ: tam giác vuông oab in o
= & gt; oa2 + ob2 = ab2
– tính chất 3: trong một tam giác vuông, đường trung tuyến của cạnh huyền bằng nửa cạnh huyền.
ví dụ: tam giác vuông oab tại o với m là trung điểm của ab
= & gt; tháng = ma = mb = ab
3. cách chứng minh tam giác vuông
– cách 1: Chứng minh tam giác có 2 góc nhọn phụ nhau.
ví dụ: hình tam giác oab có góc a + b = 90 °
= & gt; tam giác vuông góc oab tại o
– Phương pháp 2: Chứng minh rằng bình phương độ dài 1 cạnh bằng tổng bình phương độ dài 2 cạnh còn lại.
ví dụ: hình tam giác oab có oa2 + ob2 = ab2
= & gt; tam giác vuông góc oab tại o
– Phương pháp 3: Chứng minh rằng tam giác có trung tuyến tương ứng với một cạnh bằng nửa cạnh đó.
ví dụ: tam giác oab với m là trung điểm của ab, bạn biết mo = ma = mb = ½ ab
= & gt; tam giác vuông góc oab tại o
– Phương pháp 4: Chứng minh rằng tam giác nội tiếp đường tròn và có một cạnh là đường kính.
ví dụ: tam giác oab nội tiếp theo chu vi đường kính ab
= & gt; tam giác vuông góc oab tại o
Kết luận: Gia sư Tiếng Việt đã cung cấp cho người đọc định nghĩa, tính chất & amp; cách chứng minh tam giác đặc biệt trong hình học lớp 7. Hi vọng đây sẽ là nguồn tài liệu quý giúp các em nắm kiến thức và ôn luyện hiệu quả. Ngoài ra, nếu quý phụ huynh cần gia sư toán tại hà nội để giúp con em mình học tốt hơn, hãy liên hệ đến số 096.446.0088 – 090.462.8800 . chúng tôi sẵn sàng lắng nghe, từ đó tư vấn và giúp gia đình lựa chọn giải pháp tối ưu nhất.
tham khảo:
♦ Bạn có nên thuê gia sư cho con mất gốc, thiếu kỹ năng toán học không?
♦ cách hiệu quả nhất để học 7 phương trình đáng nhớ nhất
Xem ngay: Tại Sao Ổ Đĩa C Có Màu Đỏ
Vậy là đến đây bài viết về Định nghĩa, tính chất & cách chứng minh các Tam giác đặc biệt đã dừng lại rồi. Hy vọng bạn luôn theo dõi và đọc những bài viết hay của chúng tôi trên website VCCIDATA.COM.VN
Chúc các bạn luôn gặt hái nhiều thành công trong cuộc sống!
